# Condensed Matter Physics
These notes were written for the class PHY 801 at Michigan State University in Spring 2026 taught by [Philip Crowley](https://directory.natsci.msu.edu/Directory/Profiles/Person/105521) ([orcid](https://orcid.org/0000-0002-9836-7569), [google scholar](https://scholar.google.com/citations?user=FvCmptAAAAAJ&hl=en)).
#### Primary texts for the course
- Simon, "The Oxford Solid State Basicsˮ
- Ashcroft and Mermin, "Solid State Physicsˮ
#### Other good books that may serve as useful points of reference
- Kittel, "Introduction to Solid State Physicsˮ
- Girvin and Yang, “Modern Condensed Matter Physicsˮ
#### Useful online resources
- Delft open-source courses
- Akhmerov and van der Sar, “Open Solid State Notesˮ
- Akhmerov, Sau and van Heck, “Topology in Condensed Matter: Tying Quantum Knotsˮ
- Hyperphyiscs - The Physics of Solid State
- MIT OpenCourseWare - Physics for Solid-State Applications
- Dan Arovas - Lecture Notes on Condensed Matter Physics (a Work in Progress)
- Steve Simon - Resources for those using the Oxford Solid State Basics
- [Statistical Mechanics - My personal notes](https://kaedon.net/l/rpch)
- [Condensed Matter Physics (2022) - My personal notes from an undergraduate level class](https://dracentis.github.io/pdfs/CondensedMatter.pdf)
#### Problem Sets:
[Problem_set_1.pdf](https://kaedon.net/l/3p4e)
[Problem_set_2.pdf](https://kaedon.net/l/w10n)
#### Lecture Notes:
[Part 1 - Heat capacity.pdf](https://kaedon.net/l/ac76)
[Part 1 - Slides.pdf](https://kaedon.net/l/w1tk)
[Part 2 - Drude-Lorentz theory.pdf](https://kaedon.net/l/kjk5)
[Part 2 - Slides.pdf](https://kaedon.net/l/8nja)
[Part 2 - Supplementary Note.pdf](https://kaedon.net/l/t4zf)
These notes are very closely related to [Statistical Mechanics](https://kaedon.net/l/^rpch). However, there are some notable notation differences between the two texts. Some of these differences include: total energy $U$ instead of $E$, multiplicity function $W$ instead of $\Omega$ and many others. The texts are self consistent, but cross comparison should be done carefully.
## 1 Heat Capcity
### 1.1 Fundamental Statistical Mechanics
**Definition 1.1.1 ** **Energy** denoted $U$ with SI unit Joules (J) is a conserved quantity that is transferred between systems by [work](https://kaedon.net/l/^d2z2) and [heat](https://kaedon.net/l/^h7n0).
**Definition 1.1.2 ** **Work** is energy transferred to a system by macroscopic forces.
**Definition 1.1.3 ** **Heat** is energy transferred to a system by microscopic forces.
**Definition 1.1.4 ** The **multiplicity function** $W$ of a system is the number of possible microstates for a given macrostate.
**Definition 1.1.5 ** The **Boltzmann constant** denoted $k_B$ is the the proportionality factor fixed at exactly $k_B=1.380649\times 10^{-23}\text{J}/\text{K}$ that defines temperature as it is related to the statistical probability of energy states in a system.
**Definition 1.1.6 ** The **Plank constant** denoted $h$ is the proportionality factor fixed at exactly $h=6.62607015\times10^{-34}\text{J}/\text{Hz}$ relating a photon's energy to it's frequency.
**Definition 1.1.7 ** The **reduced Plank constant** denoted $\hbar=h/2\pi$ where $h$ is the [Plank constant](https://kaedon.net/l/nz1e).
**Definition 1.1.8 ** The **enthalpy** is a state function $H$ defined for total energy $U$, pressures $\mathbf{P}$ and volumes $\mathbf{V}$.
\[H = U+\mathbf{P}\cdot\mathbf{V}\]
**Definition 1.1.9 ** The **Helmholtz free energy** is a state function $F$ defined for total energy $U$, pressures $\mathbf{P}$ and volumes $\mathbf{V}$.
\[F = U-TS\]
**Definition 1.1.10 ** The **entropy** $S$ of a system is the Boltzmann constant times the natural log of the multiplicity function.
\[S = k_B\log W\]
**Definition 1.1.11 ** The **temperature** $T$ in units of kelvin (K) and **thermodynamic temperature** $\beta$ in units of joules (J) of a system are defined in terms of the derivative of energy $U$ with respect to entropy $S$.
\[T = \frac{\partial U}{\partial S} = \frac{1}{k_B\beta},\quad\beta = \frac{1}{k_B}\frac{\partial S}{\partial U} = \frac{1}{k_B T}\]
**Definition 1.1.12 ** The **microcanonical ensemble** is the ensemble of statistical mechanics where the macrostates are described by the total energy $U$, volumes $\mathbf{V}$ and particle numbers $\mathbf{N}$. The probability of each possible microstate $\mathscr{p}_i$ is assumed to be the same, so it is simply one over the multiplicity function $W$, which can be written exactly as the number of states that match the macrostate. The [canonical ensemble](https://kaedon.net/l/^kjk0#r449) and the [grand canonical ensemble](https://kaedon.net/l/^kjk0#829f) can be derived by considering a system inside a large reservoir in the microcanonical ensemble.
\[\mathscr{p}_i = \frac{1}{W(U,\mathbf{V},\mathbf{N})}\]
**Definition 1.1.13 ** The **canonical ensemble** is the ensemble of statistical mechanics where the macrostates are described by the temperature $T$, volumes $\mathbf{V}$ and particles numbers $\mathbf{N}$. The probability of a particular microstate $i$ is written in terms of the energy of the microstate $E_i$, the thermodynamic temperature $\beta$ and the **partition function** $z$.
\[\mathscr{p}_i = \frac{1}{W(T,\mathbf{V},\mathbf{N})}=\frac{e^{-\beta E_i}}{\sum_{j}{e^{-\beta E_j}}} = \frac{e^{-\beta E_i}}{z}\]
\[z = \sum_{j}{e^{-\beta E_j}} = \sum_{j}{e^{-E_j/(k_BT)}}\]
**Definition 1.1.14 ** The **canonical total energy** U of a system in the canonical ensemble is the ensemble average of the total energy of the system.
\[U = \sum_{i}{E_i \mathscr{p}_i} = \frac{1}{z}\sum_{i}{\frac{-\partial}{\partial \beta}e^{-\beta E_i}} = -\frac{1}{z}\frac{\partial z}{\partial \beta} = -\frac{\partial}{\partial \beta}\log z\]
**Definition 1.1.15 ** The **grand-canonical ensemble** is the ensemble of statistical mechanics where the macrostates are described by the temperature $T$, volumes $\mathbf{V}$, and chemical potentials $\mathbf{\mu}$. The probability of a particular microstate $i$ is written in terms of the energy of the microstate $E_i$, the particle numbers of the microstate $\mathbf{N}_i$, the thermodynamic temperature $\beta$, the chemical potentials $\mathbf{\mu}$ and the **grand partition function** $\mathscr{z}$.
\[\mathscr{p}_i = \frac{1}{W(\mathbf{T},\mathbf{V},\mathbf{\mu})}=\frac{e^{-\beta(E_i-\mathbf{\mu}\cdot\mathbf{N}_i)}}{\sum_\mathbf{N}{\sum_j{e^{-\beta(E_j-\mathbf{\mu}\cdot\mathbf{N})}}}}=\frac{e^{-\beta(E_i-\mathbf{\mu}\cdot\mathbf{N}_i)}}{\mathscr{z}}\]
\[\mathscr{z} = \sum_\mathbf{N}{\sum_j{e^{-\beta(E_j-\mathbf{\mu}\cdot\mathbf{N})}}}\]
### 1.2 Boltzmann Solids
**Definition 1.2.1 ** **Energy** denoted $U$ with SI unit Joules (J) is a conserved quantity that is transferred between systems by [work](https://kaedon.net/l/^d2z2) and [heat](https://kaedon.net/l/^h7n0).
**Definition 1.2.2 ** The **heat capacity** denoted $C$ is the derivative of total energy $U$ in terms of temperature $T$ of a system.
\[C = \frac{\partial U}{\partial T}\]
**Definition 1.2.3 ** The **heat capacity at constant pressure** denoted $C_P$ is the derivative of total enthalpy $H$ in terms of temperature $T$ of a system while pressure $P$ is held constant.
\[C_P = \left(\frac{\partial H}{\partial T}\right)_P\]
**Definition 1.2.4 ** The **heat capacity at constant volume** denoted $C_V$ is the derivative of total energy $U$ in terms of temperature $T$ of a system while pressure $V$ is held constant.
\[C_V = \left(\frac{\partial U}{\partial T}\right)_V\]
**Definition 1.2.5 ** The **coefficient of thermal expansion** denoted $\alpha$ is the derivative of volume $V$ in terms of temperature $T$ of a system while pressure $P$ is held constant divided by the volume of the system.
\[\alpha = \frac{1}{V}\left(\frac{\partial V}{\partial T}\right)_P>0\]
**Definition 1.2.6 ** The **isothermal compressibility** denoted $\kappa$ is the negative derivative of volume $V$ in terms of pressure $P$ of a system while temperature $T$ is held constant divided by the volume of the system.
\[\kappa = -\frac{1}{V}\left(\frac{\partial V}{\partial P}\right)_T>0\]
**Result 1.2.7 ** **Mayer's relation** states that the [heat capacity at constant pressure](https://kaedon.net/l/5tja) $C_P$ and [heat capacity at constant volume](https://kaedon.net/l/79an) $C_V$ must differ by a positive nonzero value determined by the temperature $T$, volume $V$, [coefficient of thermal expansion](https://kaedon.net/l/^kjk0#mpdm) $\alpha$ and [isothermal compressibility](https://kaedon.net/l/5kpm) $\kappa$ of the system.
\[C_P-C_V = \frac{TV\alpha^2}{\kappa}= -T\left(\frac{\partial V}{\partial T}\right)^2_P\left(\frac{\partial P}{\partial V}\right)_T>0\]
**Definition 1.2.8 ** An **intensive quantity** is a variable of a system that *does not* scale with the size of the system.,
**Definition 1.2.9 ** An **extensive quantity** is a variable of a system that *does* scale with the size of the system.
**Definition 1.2.10 ** The **specific heat** denoted $c$ is the derivative of total energy $U$ in terms of temperature $T$ scaled per unit mass $M$ of the system such that it is an [intensive quantity](https://kaedon.net/l/9wj5).
\[c = \frac{C}{M} = \frac{1}{M}\frac{\partial U}{\partial T}\]
**Definition 1.2.11 ** The **molar specific heat** denoted $c_{mol}$ is the derivative of total energy $U$ in terms of temperature $T$ scaled to the number of moles $N_{mol}$ in the system such that it is an [intensive quantity](https://kaedon.net/l/9wj5). It can also be defined in terms of the [specific heat](https://kaedon.net/l/cna6) $c$ and molar mass $m_{mol}$.
\[c_{mol} = \frac{C}{N_{mol}} = \frac{c}{m_{mol}} = \frac{1}{N_{mol}}\frac{\partial U}{\partial T}\]
**Definition 1.2.12 ** The **Boltzmann solid** is a classical model of solids in the canonical ensemble that models the valence electrons of atoms as classical particles in potential wells with the following Hamiltonian $H$, where $\vec{p}$ is the momentum, $m$ is the mass, $k$ is the spring constant and $\vec{x}$ is position of the electron relative to the center of the potential well.
\[H = \frac{p^2}{2m}+\frac{1}{2}kx^2\]
\[\mathscr{p}(\vec{x},\vec{p}) = \frac{e^{-\beta H(\vec{x},\vec{p})}}{z},\quad z = \int d^3\vec{x}\int d^3\vec{p} e^{-\beta H(\vec{x},\vec{p})}\]
**Result 1.2.13 ** The **intensive energy of a Boltzmann solid** $u$ is the average energy per particle in a 3d solid determined by the following relation with temperature $T$.
\[u = -\frac{\partial}{\partial \beta}\log z = 3k_BT\]
**Law 1.2.14 ** The **Dulong Petit law** states that the [molar specific heat](https://kaedon.net/l/^kjk0#fm30) for most bulk materials is a constant at high temperatures.
\[C = N_{atoms}\frac{\partial u}{\partial T} = 3k_BN_{atoms}\]
\[c_{mol}=\frac{C}{N_{mol}}=\frac{3k_BN_{atoms}}{N_{mol}} = 3k_BN_{Avogadro} = 3R\]
**Figure 1.2.15 Dulong Petit Law Figure **
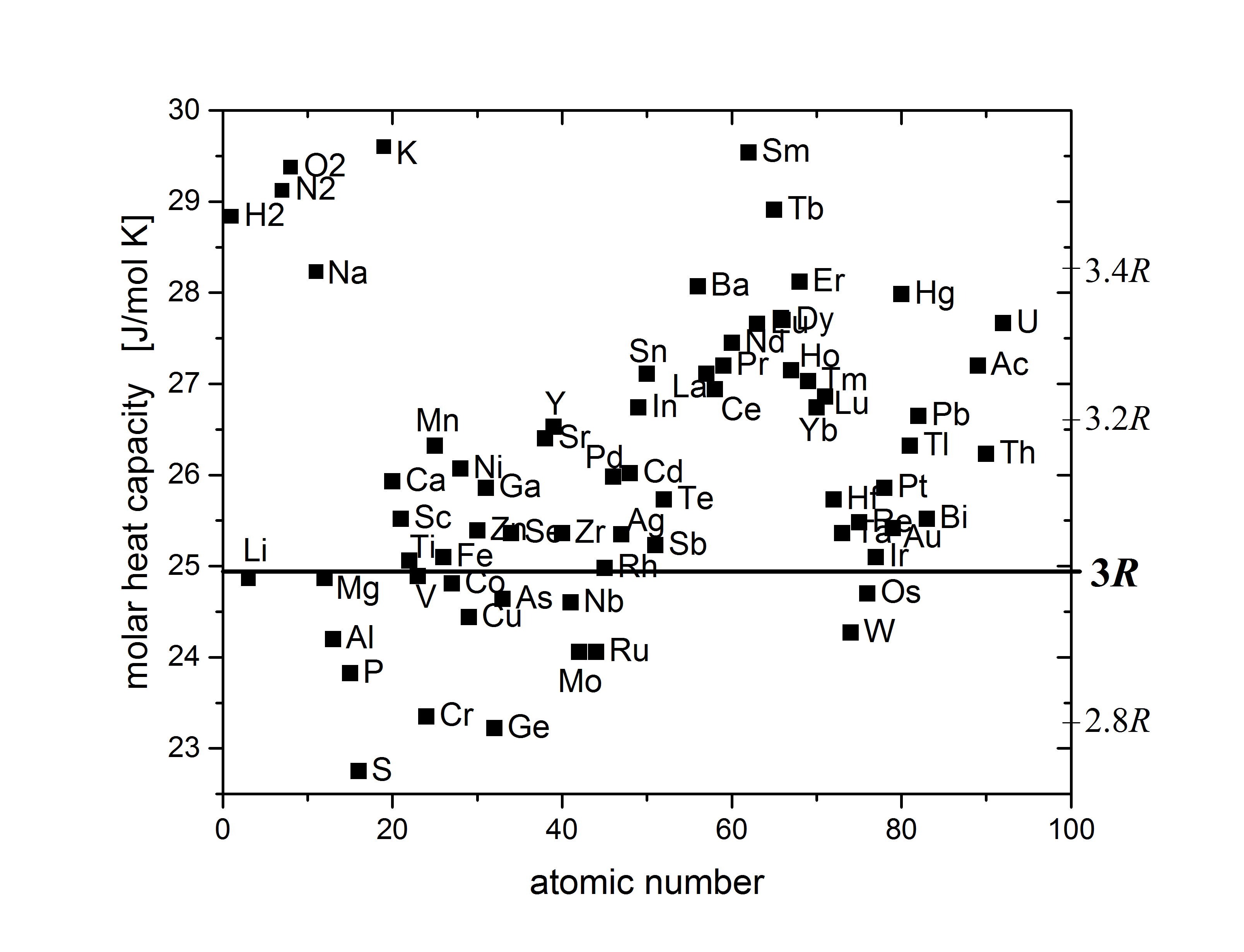 Molar heat capacity of most elements at 25 °C is in the range between 2.8 R and 3.4 R: Plot as a function of atomic number with a y range from 22.5 to 30 J/mol K. By Nick B. - Own work, CC BY-SA 4.0, Link
**File 1.2.15 ** GraphHeatCapacityElements_SelectedRange.png
### 1.3 Einstein Solids
**Definition 1.3.1 ** The **Einstein solid** is a quantum model of solids in the canonical ensemble that models the valence electrons of atoms as quantum harmonic oscillators with the following Hamiltonian $H$, where $\hat{p}$ is the momentum operator, $m$ is the mass, $k$ is the spring constant and $\hat{x}$ is the position operator.
\[\hat{H} = \frac{\hat{p}^2}{2m}+\frac{1}{2}k\hat{x}^2\]
**Result 1.3.2 ** The **eigenvalues of the 1D Harmonic oscillator** $E_n$ for the corresponding eigenstates $\ket{n}$ are given by the following equation for non-negative integer $n\in\mathbb{N}$.
\[E_n = \hbar\omega\left(n+\frac{1}{2}\right),\quad H\ket{n} = E_n\ket{n}, \quad \omega = \sqrt\frac{k}{m}\]
**Proposition 1.3.3 ** **Geometric series convergence** states that for $|r|<1$ the following infinite series converges to $1/(1-r)$.
\[\sum_{k=0}^\infty{r^k} = \frac{1}{1-r}\]
**Result 1.3.4 ** The **partition function of a 1D harmonic oscillator** $z_{1D}$ can be written as a geometric series:
\[z_{1D} = \sum_{n=0}^\infty{e^{-\beta E_n}} = \sum_{n=0}^\infty{e^{-\beta\hbar\omega(n+\frac{1}{2})}} = \frac{e^{\beta\hbar\omega/2}}{e^{\beta\hbar\omega}-1}\]
**Result 1.3.5 ** The **eigenvalues of the 3D Harmonic oscillator** $E_{n_x,n_y,n_z}$ for the corresponding eigenstates $\ket{n_x,n_y,n_z}$ are given by the following equation for non-negative integers $n_x,n_y,n_z\in\mathbb{N}$.
\[E_{n_x,n_y,n_z} = \hbar\omega\left(n_x+n_y+n_z+\frac{3}{2}\right)\]
\[H\ket{n_z,n_y,n_z} = E_{n_z,n_y,n_z}\ket{n}\]
\[\omega = \sqrt\frac{k}{m}\]
**Result 1.3.6 ** The **partition function of a 3D harmonic oscillator** $z_{3D}$ can be written in terms of the partition function for the 1D harmonic oscillator $z_{1D}$:
\[z_{3D} = \sum_{n_x,n_y,n_z=0}^\infty{e^{-\beta E_{n_x,n_y,n_z}}} = z_{1D}^3 = \left(\frac{e^{\beta\hbar\omega/2}}{e^{\beta\hbar\omega}-1}\right)^3\]
**Definition 1.3.7 ** The **Bose factor** is $n_B(\beta\hbar\omega) = \frac{1}{e^{\beta\hbar\omega}-1}$.
**Result 1.3.8 ** The **intensive energy of a Einstein solid** $u$ is the average energy per particle in a 3d solid determined by the following relation with temperature $T$.
\[u = -\frac{\partial}{\partial \beta}\log z_{3D} = -3\frac{\partial}{\partial \beta}\log z_{1D} \]
\[= 3\hbar\omega \left(n_B(\beta\hbar\omega)+\frac{1}{2} \right) = 3\hbar\omega \left( \frac{1}{e^{\beta\hbar\omega}-1} + \frac{1}{2} \right)\]
**Result 1.3.9 ** The **molar heat capacity of an Einstain solid** $u_{mol}$ satisfies the [Dulong Petit law](https://kaedon.net/l/5cdh) at high temperatures as $T\to\infty$ while converging to zero as $T\to0$.
\[u_{mol} = \frac{C}{N_{mol}} = N_{Avogadro}\frac{\partial u}{\partial T} = 3R(\beta\hbar\omega)^2\frac{e^{\beta\hbar\omega}}{\left( e^{\beta\hbar\omega}-1 \right)^2}\]
**Definition 1.3.10 ** The **einstein temperature** denoted $T_E$ is the critical temperature where the molar heat capacity of an Einstein solid starts decreasing.
\[T_E = \frac{\hbar\omega}{k_B}\]
**Figure 1.3.11 Molar Heat Capacity of an Einstein Solid vs Temperature **
Molar heat capacity of most elements at 25 °C is in the range between 2.8 R and 3.4 R: Plot as a function of atomic number with a y range from 22.5 to 30 J/mol K. By Nick B. - Own work, CC BY-SA 4.0, Link
**File 1.2.15 ** GraphHeatCapacityElements_SelectedRange.png
### 1.3 Einstein Solids
**Definition 1.3.1 ** The **Einstein solid** is a quantum model of solids in the canonical ensemble that models the valence electrons of atoms as quantum harmonic oscillators with the following Hamiltonian $H$, where $\hat{p}$ is the momentum operator, $m$ is the mass, $k$ is the spring constant and $\hat{x}$ is the position operator.
\[\hat{H} = \frac{\hat{p}^2}{2m}+\frac{1}{2}k\hat{x}^2\]
**Result 1.3.2 ** The **eigenvalues of the 1D Harmonic oscillator** $E_n$ for the corresponding eigenstates $\ket{n}$ are given by the following equation for non-negative integer $n\in\mathbb{N}$.
\[E_n = \hbar\omega\left(n+\frac{1}{2}\right),\quad H\ket{n} = E_n\ket{n}, \quad \omega = \sqrt\frac{k}{m}\]
**Proposition 1.3.3 ** **Geometric series convergence** states that for $|r|<1$ the following infinite series converges to $1/(1-r)$.
\[\sum_{k=0}^\infty{r^k} = \frac{1}{1-r}\]
**Result 1.3.4 ** The **partition function of a 1D harmonic oscillator** $z_{1D}$ can be written as a geometric series:
\[z_{1D} = \sum_{n=0}^\infty{e^{-\beta E_n}} = \sum_{n=0}^\infty{e^{-\beta\hbar\omega(n+\frac{1}{2})}} = \frac{e^{\beta\hbar\omega/2}}{e^{\beta\hbar\omega}-1}\]
**Result 1.3.5 ** The **eigenvalues of the 3D Harmonic oscillator** $E_{n_x,n_y,n_z}$ for the corresponding eigenstates $\ket{n_x,n_y,n_z}$ are given by the following equation for non-negative integers $n_x,n_y,n_z\in\mathbb{N}$.
\[E_{n_x,n_y,n_z} = \hbar\omega\left(n_x+n_y+n_z+\frac{3}{2}\right)\]
\[H\ket{n_z,n_y,n_z} = E_{n_z,n_y,n_z}\ket{n}\]
\[\omega = \sqrt\frac{k}{m}\]
**Result 1.3.6 ** The **partition function of a 3D harmonic oscillator** $z_{3D}$ can be written in terms of the partition function for the 1D harmonic oscillator $z_{1D}$:
\[z_{3D} = \sum_{n_x,n_y,n_z=0}^\infty{e^{-\beta E_{n_x,n_y,n_z}}} = z_{1D}^3 = \left(\frac{e^{\beta\hbar\omega/2}}{e^{\beta\hbar\omega}-1}\right)^3\]
**Definition 1.3.7 ** The **Bose factor** is $n_B(\beta\hbar\omega) = \frac{1}{e^{\beta\hbar\omega}-1}$.
**Result 1.3.8 ** The **intensive energy of a Einstein solid** $u$ is the average energy per particle in a 3d solid determined by the following relation with temperature $T$.
\[u = -\frac{\partial}{\partial \beta}\log z_{3D} = -3\frac{\partial}{\partial \beta}\log z_{1D} \]
\[= 3\hbar\omega \left(n_B(\beta\hbar\omega)+\frac{1}{2} \right) = 3\hbar\omega \left( \frac{1}{e^{\beta\hbar\omega}-1} + \frac{1}{2} \right)\]
**Result 1.3.9 ** The **molar heat capacity of an Einstain solid** $u_{mol}$ satisfies the [Dulong Petit law](https://kaedon.net/l/5cdh) at high temperatures as $T\to\infty$ while converging to zero as $T\to0$.
\[u_{mol} = \frac{C}{N_{mol}} = N_{Avogadro}\frac{\partial u}{\partial T} = 3R(\beta\hbar\omega)^2\frac{e^{\beta\hbar\omega}}{\left( e^{\beta\hbar\omega}-1 \right)^2}\]
**Definition 1.3.10 ** The **einstein temperature** denoted $T_E$ is the critical temperature where the molar heat capacity of an Einstein solid starts decreasing.
\[T_E = \frac{\hbar\omega}{k_B}\]
**Figure 1.3.11 Molar Heat Capacity of an Einstein Solid vs Temperature **
 Molar heat capacity predicted for an Einstein solid as a function of temperature. Public Domain, own work.
**File 1.3.11 ** MolarHeatCapacityofanEinstainSolidvsTemperature.svg
### 1.4 Debye Solids
Also see the Wikipedia article for this model: https://en.wikipedia.org/wiki/Debye_model
**Definition 1.4.1 ** The **Debye solid** is a model of solids in the canonical ensemble that models the collective phononic collective modes the atoms in the solid for some speed of sound $v$, the frequencies of the collect modes $\omega_k$ for wave number $\vec{k}$ are modeled by the following equations for the total energy $U$.
\[\omega_\vec{k} = v\abs{\vec{k}}\]
\[U = 3\sum_\vec{k}\hbar\omega_\vec{k}\left( n_B(\beta\hbar\omega_\vec{k}) + \frac{1}{2} \right) = 3\sum_\vec{k}\hbar\omega_\vec{k}\left( \frac{1}{e^{\beta\hbar\omega_\vec{k}}-1} + \frac{1}{2} \right)\]
**Definition 1.4.2 ** To calculate the modes of a Debye solid we assume **periodic boundary conditions** for some distance $L$ which is very large compared to the scale of the atom as to include all the lower frequency modes.
\[\vec{k}L = 2\pi\vec{n}\]
**Definition 1.4.3 ** The **Debye frequency** denoted $\omega_D$ is the maximum frequency of phonons in a Debye solid, defined in terms of the density $\rho$ and speed of sound $v$ of the solid.
\[\omega_D = \left(6\pi^2\rho\right)^{1/3}v\]
**Definition 1.4.4 ** The **Debye temperature** is $T_D = \frac{\hbar\omega_D}{k_B}$ where $\omega_D$ is the [debye frequency](https://kaedon.net/l/76mk).
**Definition 1.4.5 ** The **Debye density of states** denoted $g(\omega)$ of frequency modes $\omega$ with periodic boundary conditions $L$ and volume $V$ is the following function.
\[g(\omega) = \frac{L^3\omega^2}{2\pi^2V^3} = \frac{3N\omega^2}{\omega_D^3}\]
**Result 1.4.6 ** The sum of an isotropic function $f(\omega_{k})$ for all wave numbers $\vec{k}$ can be approximated as an integral of the density of states $g(\omega_{\vec{k}})$ and the function $f(\omega_{\vec{k}})$.
\[\sum_{\vec{k}}f(\omega_\vec{k})=\sum_\vec{k}f(v\abs{\vec{k}})=\sum_{\vec{n}\in\mathbb{N}^3}f\left(\frac{2\pi v}{L}\abs{\vec{n}}\right)\]
\[\approx\int d^3\vec{n} f\left(\frac{2\pi v}{L}\abs{\vec{n}}\right) = \left(\frac{L}{2\pi}\right)^3\int d^3\vec{k}f\left(v\abs{\vec{k}}\right)\]
\[= \frac{L^3}{2\pi^2}\int_0^{\omega_D} dk k^2 f(vk) = \frac{L^3}{2\pi^2 v^3}\int_0^{\omega_D} d\omega \omega^2 f(\omega) = \int_0^{\omega_D} d\omega g(\omega) f(\omega)\]
We set the maximum frequency of the integrate to $\omega_D$ because there are a finite number of atoms $N$. It turns out that there is a maximum frequency $\omega$ that these collective modes can exhibit. The next result proves that this cutoff frequency is indeed the [Debye frequency](https://kaedon.net/l/76mk) $\omega_D$.
**Result 1.4.8 ** The [Debye frequency](https://kaedon.net/l/^kjk0#76mk) is the maximum frequency in a Debye solid, because there are a finite number of atoms $N$ in a solid.
\[N = \sum_k 1 = \int_0^{\omega_D} d\omega g(\omega) = \int_0^{\omega_D} d\omega \frac{3N\omega^2}{\omega_D^3} = N\frac{\omega_D^3}{\omega_D^3} = N\]
**Result 1.4.9 ** The **total energy** $U$ **of a Debye solid** is given by the following integral of the [Debye density of states](https://kaedon.net/l/^kjk0#7n9k) $g(\omega)$ and the [Bose factor](https://kaedon.net/l/^kjk0#c06t) $n_B(\beta\hbar\omega)$.
\[U = \int_0^{\omega_D} d\omega g(\omega) 3\hbar\omega\left( n_B(\beta\hbar\omega) + \frac{1}{2} \right) = \int_0^{\omega_D} d\omega \frac{3N\omega^2}{\omega_D^3} 3\hbar\omega\left( \frac{1}{e^{\beta\hbar\omega}-1} + \frac{1}{2} \right)\]
**Result 1.4.10 ** The **molar heat capacity** $c_{mol}$ **of a Debye solid** is given by the following integral.
\[c_{mol} = \frac{1}{N_{mol}}\frac{\partial U}{\partial T} = \frac{1}{N_{mol}}\frac{\partial}{\partial T}\int_0^{\omega_D} d\omega g(\omega) 3\hbar\omega\left( n_B(\beta\hbar\omega) + \frac{1}{2} \right) \]
\[= \frac{1}{N_{mol}}\frac{\partial}{\partial T}\int_0^{\omega_D} d\omega \frac{3N\omega^2}{\omega_D^3} 3\hbar\omega\left( \frac{1}{e^{\beta\hbar\omega}-1} + \frac{1}{2} \right)\]
**Figure 1.4.11 Debye vs. Einstein **
Molar heat capacity predicted for an Einstein solid as a function of temperature. Public Domain, own work.
**File 1.3.11 ** MolarHeatCapacityofanEinstainSolidvsTemperature.svg
### 1.4 Debye Solids
Also see the Wikipedia article for this model: https://en.wikipedia.org/wiki/Debye_model
**Definition 1.4.1 ** The **Debye solid** is a model of solids in the canonical ensemble that models the collective phononic collective modes the atoms in the solid for some speed of sound $v$, the frequencies of the collect modes $\omega_k$ for wave number $\vec{k}$ are modeled by the following equations for the total energy $U$.
\[\omega_\vec{k} = v\abs{\vec{k}}\]
\[U = 3\sum_\vec{k}\hbar\omega_\vec{k}\left( n_B(\beta\hbar\omega_\vec{k}) + \frac{1}{2} \right) = 3\sum_\vec{k}\hbar\omega_\vec{k}\left( \frac{1}{e^{\beta\hbar\omega_\vec{k}}-1} + \frac{1}{2} \right)\]
**Definition 1.4.2 ** To calculate the modes of a Debye solid we assume **periodic boundary conditions** for some distance $L$ which is very large compared to the scale of the atom as to include all the lower frequency modes.
\[\vec{k}L = 2\pi\vec{n}\]
**Definition 1.4.3 ** The **Debye frequency** denoted $\omega_D$ is the maximum frequency of phonons in a Debye solid, defined in terms of the density $\rho$ and speed of sound $v$ of the solid.
\[\omega_D = \left(6\pi^2\rho\right)^{1/3}v\]
**Definition 1.4.4 ** The **Debye temperature** is $T_D = \frac{\hbar\omega_D}{k_B}$ where $\omega_D$ is the [debye frequency](https://kaedon.net/l/76mk).
**Definition 1.4.5 ** The **Debye density of states** denoted $g(\omega)$ of frequency modes $\omega$ with periodic boundary conditions $L$ and volume $V$ is the following function.
\[g(\omega) = \frac{L^3\omega^2}{2\pi^2V^3} = \frac{3N\omega^2}{\omega_D^3}\]
**Result 1.4.6 ** The sum of an isotropic function $f(\omega_{k})$ for all wave numbers $\vec{k}$ can be approximated as an integral of the density of states $g(\omega_{\vec{k}})$ and the function $f(\omega_{\vec{k}})$.
\[\sum_{\vec{k}}f(\omega_\vec{k})=\sum_\vec{k}f(v\abs{\vec{k}})=\sum_{\vec{n}\in\mathbb{N}^3}f\left(\frac{2\pi v}{L}\abs{\vec{n}}\right)\]
\[\approx\int d^3\vec{n} f\left(\frac{2\pi v}{L}\abs{\vec{n}}\right) = \left(\frac{L}{2\pi}\right)^3\int d^3\vec{k}f\left(v\abs{\vec{k}}\right)\]
\[= \frac{L^3}{2\pi^2}\int_0^{\omega_D} dk k^2 f(vk) = \frac{L^3}{2\pi^2 v^3}\int_0^{\omega_D} d\omega \omega^2 f(\omega) = \int_0^{\omega_D} d\omega g(\omega) f(\omega)\]
We set the maximum frequency of the integrate to $\omega_D$ because there are a finite number of atoms $N$. It turns out that there is a maximum frequency $\omega$ that these collective modes can exhibit. The next result proves that this cutoff frequency is indeed the [Debye frequency](https://kaedon.net/l/76mk) $\omega_D$.
**Result 1.4.8 ** The [Debye frequency](https://kaedon.net/l/^kjk0#76mk) is the maximum frequency in a Debye solid, because there are a finite number of atoms $N$ in a solid.
\[N = \sum_k 1 = \int_0^{\omega_D} d\omega g(\omega) = \int_0^{\omega_D} d\omega \frac{3N\omega^2}{\omega_D^3} = N\frac{\omega_D^3}{\omega_D^3} = N\]
**Result 1.4.9 ** The **total energy** $U$ **of a Debye solid** is given by the following integral of the [Debye density of states](https://kaedon.net/l/^kjk0#7n9k) $g(\omega)$ and the [Bose factor](https://kaedon.net/l/^kjk0#c06t) $n_B(\beta\hbar\omega)$.
\[U = \int_0^{\omega_D} d\omega g(\omega) 3\hbar\omega\left( n_B(\beta\hbar\omega) + \frac{1}{2} \right) = \int_0^{\omega_D} d\omega \frac{3N\omega^2}{\omega_D^3} 3\hbar\omega\left( \frac{1}{e^{\beta\hbar\omega}-1} + \frac{1}{2} \right)\]
**Result 1.4.10 ** The **molar heat capacity** $c_{mol}$ **of a Debye solid** is given by the following integral.
\[c_{mol} = \frac{1}{N_{mol}}\frac{\partial U}{\partial T} = \frac{1}{N_{mol}}\frac{\partial}{\partial T}\int_0^{\omega_D} d\omega g(\omega) 3\hbar\omega\left( n_B(\beta\hbar\omega) + \frac{1}{2} \right) \]
\[= \frac{1}{N_{mol}}\frac{\partial}{\partial T}\int_0^{\omega_D} d\omega \frac{3N\omega^2}{\omega_D^3} 3\hbar\omega\left( \frac{1}{e^{\beta\hbar\omega}-1} + \frac{1}{2} \right)\]
**Figure 1.4.11 Debye vs. Einstein **
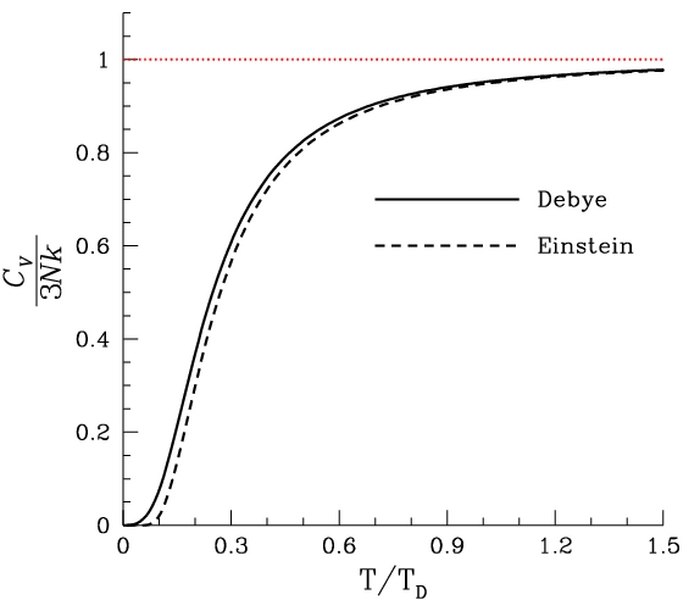 Predicted heat capacity as a function of temperature. Public Domain, Link
**File 1.4.11 ** DebyeVSEinstein.jpg
## 2 Drude-Lorentz Theory
### 2.1 Drude Model
**Definition 2.1.1 ** The **Drude model** is a simple model of electron motion and scattering in a material with a differential equation describing of the momentum $\vec{p}$ of electrons experiencing the Lorentz force from an external electric field $\vec{E}$, magnetic field $\vec{B}$ and scattering with a mean scattering time of $\tau$.
\[\frac{\partial \vec{p}}{\partial t} = -e\left( \vec{E} + \frac{1}{m}\vec{p}\times\vec{B} \right) + \frac{\vec{p}}{\tau}\]
Despite the apparent simplicity of the [Drude Model](https://kaedon.net/l/73pc), it has been wildly successful at predicting a variety of phenomena related to electron transport in solids. Some of these phenomena include:
- [Ohm's Law](https://kaedon.net/l/d4em)
- [The Hall Effect](https://kaedon.net/l/pt5f)
The following sections will describe each of these phenomena using the [Drude Model](https://kaedon.net/l/73pc). The drude model can then also be expanded into a complete thermodynamic theory for electrons with the [Drude-Lorentz gas](https://kaedon.net/l/tf4d). Which allows it to at least conceptually explain the following phenomena:
- [Weidermann's Franz Law](https://kaedon.net/l/tf4d)
- [Transparency of Materials](https://kaedon.net/l/^kjk0#6kn0)
### 2.2 Ohm's Law
**Definition 2.2.1 ** A **current density** denoted $\vec{j}$ is a vector field describing the average density of charge flowing through a particular point in space per second.
**Definition 2.2.2 ** The **electric conductivity** denoted $\sigma$ of a material is the coefficient or tensor that relates the electric field $\vec{E}$ to the current density $\vec{j}$.
\[\vec{j} = \sigma \vec{E}\]
**Definition 2.2.3 ** The **resistivity** denoted $\rho$ of a material is the coefficient or tensor that relates the current density $\vec{\rho}$ flowing through a material with the electric field $\vec{E}$ required to drive that current.
\[\vec{E} = \rho\vec{j}\]
**Corollary 2.2.4 ** The [conductivity](https://kaedon.net/l/1htz) $\sigma$ and [resistivity](https://kaedon.net/l/h144) $\rho$ of a material are inverses of each other.
\[\sigma = \frac{1}{\rho},\quad \rho = \frac{1}{\sigma}\]
**Definition 2.2.5 ** The **Drude conducitivity** denoted $\sigma_D$ is the [electric conductivity](https://kaedon.net/l/^kjk0#1htz) predicted by the Drude model for a pure electric field $\vec{E}$ ($\vec{B}=\vec{0}$) where $\tau$ is the mean scattering time, $n_e$ is number of electrons, $e$ is the elemental charge and $m_e$ is the mass of charge carriers.
\[\vec{j}_D = \frac{e^2n_e\tau}{m_e}\vec{E} = \sigma_D\vec{E}\]
**Definition 2.2.6 ** The **resistance** denoted $R$ of a prism of material with cross sectional area $A$, length $L$ and resistivity $\rho$ is given by the following relation.
\[R = \rho \frac{\ell}{A}\]
Predicted heat capacity as a function of temperature. Public Domain, Link
**File 1.4.11 ** DebyeVSEinstein.jpg
## 2 Drude-Lorentz Theory
### 2.1 Drude Model
**Definition 2.1.1 ** The **Drude model** is a simple model of electron motion and scattering in a material with a differential equation describing of the momentum $\vec{p}$ of electrons experiencing the Lorentz force from an external electric field $\vec{E}$, magnetic field $\vec{B}$ and scattering with a mean scattering time of $\tau$.
\[\frac{\partial \vec{p}}{\partial t} = -e\left( \vec{E} + \frac{1}{m}\vec{p}\times\vec{B} \right) + \frac{\vec{p}}{\tau}\]
Despite the apparent simplicity of the [Drude Model](https://kaedon.net/l/73pc), it has been wildly successful at predicting a variety of phenomena related to electron transport in solids. Some of these phenomena include:
- [Ohm's Law](https://kaedon.net/l/d4em)
- [The Hall Effect](https://kaedon.net/l/pt5f)
The following sections will describe each of these phenomena using the [Drude Model](https://kaedon.net/l/73pc). The drude model can then also be expanded into a complete thermodynamic theory for electrons with the [Drude-Lorentz gas](https://kaedon.net/l/tf4d). Which allows it to at least conceptually explain the following phenomena:
- [Weidermann's Franz Law](https://kaedon.net/l/tf4d)
- [Transparency of Materials](https://kaedon.net/l/^kjk0#6kn0)
### 2.2 Ohm's Law
**Definition 2.2.1 ** A **current density** denoted $\vec{j}$ is a vector field describing the average density of charge flowing through a particular point in space per second.
**Definition 2.2.2 ** The **electric conductivity** denoted $\sigma$ of a material is the coefficient or tensor that relates the electric field $\vec{E}$ to the current density $\vec{j}$.
\[\vec{j} = \sigma \vec{E}\]
**Definition 2.2.3 ** The **resistivity** denoted $\rho$ of a material is the coefficient or tensor that relates the current density $\vec{\rho}$ flowing through a material with the electric field $\vec{E}$ required to drive that current.
\[\vec{E} = \rho\vec{j}\]
**Corollary 2.2.4 ** The [conductivity](https://kaedon.net/l/1htz) $\sigma$ and [resistivity](https://kaedon.net/l/h144) $\rho$ of a material are inverses of each other.
\[\sigma = \frac{1}{\rho},\quad \rho = \frac{1}{\sigma}\]
**Definition 2.2.5 ** The **Drude conducitivity** denoted $\sigma_D$ is the [electric conductivity](https://kaedon.net/l/^kjk0#1htz) predicted by the Drude model for a pure electric field $\vec{E}$ ($\vec{B}=\vec{0}$) where $\tau$ is the mean scattering time, $n_e$ is number of electrons, $e$ is the elemental charge and $m_e$ is the mass of charge carriers.
\[\vec{j}_D = \frac{e^2n_e\tau}{m_e}\vec{E} = \sigma_D\vec{E}\]
**Definition 2.2.6 ** The **resistance** denoted $R$ of a prism of material with cross sectional area $A$, length $L$ and resistivity $\rho$ is given by the following relation.
\[R = \rho \frac{\ell}{A}\]
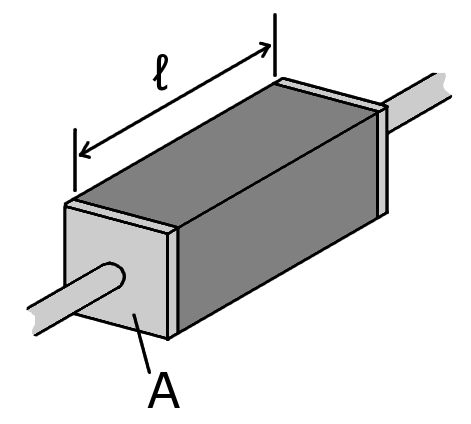 **File 2.2.6 ** Resistance_geometry.png
**Law 2.2.7 ** **Ohm's law** states that the total current $I$ flowing through a material is equal to the resistance $R$ times the bias voltage across the material $V$.
\[V = IR\]
### 2.3 The Hall Effect
**Definition 2.3.1 ** The **cyclotron frequency** denoted $\omega_c$ is the frequency at which an electron would spin in a magnetic field of strength $B$, with elemental charge $e$ and electron mass $m_e$.
\[\omega_c = \frac{eB}{m_e}\]
**Definition 2.3.2 ** The **hall effect** is the production of an electric field $\vec{E}_{\text{hall}}$ (called the **hall field**) across a material in the direction of the cross product between the external electric field $\vec{E}_{\text{ext}}$ and the magnetic field $\vec{B}$.
**Result 2.3.3 ** The **classical hall effect** is the hall effect as predicted by solving the equilibrium condition $\frac{\partial \vec{p}}{\partial t} = 0$ for the [Drude Model](https://kaedon.net/l/73pc) in 2 dimensions with a magnetic field $\vec{B}=B\hat{z}$ perpendicular to the plane and an in-plane electric field $\vec{E} = E_x\hat{x} + E_y\hat{y}$.
\[0=-eE_x - \omega_c p_y - \frac{p_x}{\tau}, \quad 0=-eE_y + \omega_c p_x - \frac{p_y}{\tau}\]
\[\vec{p} = \frac{-e\tau}{1+(\omega_c\tau)^2}\begin{pmatrix}1 & -\omega_c\tau\\ \omega_c\tau & 1\end{pmatrix}\vec{E}\]
**Figure 2.3.4 Hall Effect Diagram **
**File 2.2.6 ** Resistance_geometry.png
**Law 2.2.7 ** **Ohm's law** states that the total current $I$ flowing through a material is equal to the resistance $R$ times the bias voltage across the material $V$.
\[V = IR\]
### 2.3 The Hall Effect
**Definition 2.3.1 ** The **cyclotron frequency** denoted $\omega_c$ is the frequency at which an electron would spin in a magnetic field of strength $B$, with elemental charge $e$ and electron mass $m_e$.
\[\omega_c = \frac{eB}{m_e}\]
**Definition 2.3.2 ** The **hall effect** is the production of an electric field $\vec{E}_{\text{hall}}$ (called the **hall field**) across a material in the direction of the cross product between the external electric field $\vec{E}_{\text{ext}}$ and the magnetic field $\vec{B}$.
**Result 2.3.3 ** The **classical hall effect** is the hall effect as predicted by solving the equilibrium condition $\frac{\partial \vec{p}}{\partial t} = 0$ for the [Drude Model](https://kaedon.net/l/73pc) in 2 dimensions with a magnetic field $\vec{B}=B\hat{z}$ perpendicular to the plane and an in-plane electric field $\vec{E} = E_x\hat{x} + E_y\hat{y}$.
\[0=-eE_x - \omega_c p_y - \frac{p_x}{\tau}, \quad 0=-eE_y + \omega_c p_x - \frac{p_y}{\tau}\]
\[\vec{p} = \frac{-e\tau}{1+(\omega_c\tau)^2}\begin{pmatrix}1 & -\omega_c\tau\\ \omega_c\tau & 1\end{pmatrix}\vec{E}\]
**Figure 2.3.4 Hall Effect Diagram **
 Hall Effect Measurement Setup for Electrons. An external field $E_x$ is applied in the x direction and a magnetic field $B_z$ is applied in the z direction, resulting in a hall field $E_y$ in the y direction. Public Domain, Link
**File 2.3.4 ** Hall_Effect_Measurement_Setup_for_Electrons.svg
**Result 2.3.5 ** The **classical hall field** $\vec{E}_{\text{hall}}$ for external electric field $\vec{E}_{\text{ext}}$ and magnetic field $\vec{B}$ can be written in terms of the [cyclotron frequency](https://kaedon.net/l/k3cc) $\omega_c$ and [mean scattering time](https://kaedon.net/l/73pc) $\tau$
\[\vec{E}_{\text{hall}} = \omega_c\tau(\vec{B}\times\vec{E}_{\text{ext}})\]
**Definition 2.3.6 ** The **hall coefficient** denoted $R_H$ is the measurable ratio between the hall field $E_y$ and the product of the current $J_x$ and $B_z$ applied to drive that hall field. The Drude model predicts that this quantity is related to the charge carrier density $n_e$.
\[R_H = \frac{E_y}{J_xB_z} = \frac{-\omega_c\tau E_x}{J_x B_z} = \frac{-1}{en_e}\]
### 2.4 Drude-Lorentz Gas
**Definition 2.4.1 ** The **temperature gradient** denoted $\vec{\nabla} T(\vec{r})$ is the the gradient of temperature $T(\vec{r})$ at position $\vec{r}$ in a material.
**Definition 2.4.2 ** The **heat current** denoted $\vec{j}_q$ is the rate of energy transfer through a material due to temperature gradient.
**Definition 2.4.3 ** The **thermal conductivity** denoted $k$ of a material is the coefficient that relates the temperature gradient $\nabla T$ to the heat current $\vec{j}_q$.
\[\vec{j}_q = -k\sigma \vec{E}\]
**Definition 2.4.4 **
**Definition 2.4.5 **
**Result 2.4.6 **
**Result 2.4.7 **
**Result 2.4.8 **
**Result 2.4.9 **
**Result 2.4.10 **
**Definition 2.4.11 ** \[\text{DYNAMIC EQUATION}\]
\[\text{Equilibrium Condition}\]
**Definition 2.4.12 ** linear response coefficients
**Result 2.4.13 ** electric conductivity, heat conductivity, seabeck
**Result 2.4.14 ** Drude-Lorentz Heat capacity
**Definition 2.4.15 ** The **Lorentz number** denoted $L$ is the proportionality constant that relates the thermal conductivity $\kappa$ to the electric conductivity $\sigma$ at temperature $T$.
\[L = \frac{\kappa}{\sigma T}\]
**Law 2.4.16 ** The **Wiedemann–Franz law** states that the [Lorentz number](https://kaedon.net/l/217r) $L$ is a constant that can be written in terms of the Boltzmann constant $k_B$ and the elementary charge $e$.
\[L = \frac{\kappa}{\sigma L} = \frac{\pi^2}{3}\left( \frac{k_B}{e} \right)^2\]
### 2.5 Transparency
**Definition 2.5.1 **
### 2.6 Sommerfeld Model
**Definition 2.6.1 **
**Definition 2.6.2 **
## 3 Geometry and Constitution of Solids
**Section 3.1 **
**Section 3.2 **
**Section 3.3 **
**Section 3.4 **
## 4 Electrons in Solids
**Section 4.1 **
**Section 4.2 **
**Section 4.3 **
**Section 4.4 **
## 5 Disorder and Defects
**Section 5.1 **
**Section 5.2 **
**Section 5.3 **
## 6 Topology
**Section 6.1 **
**Section 6.2 **
**Section 6.3 **
Hall Effect Measurement Setup for Electrons. An external field $E_x$ is applied in the x direction and a magnetic field $B_z$ is applied in the z direction, resulting in a hall field $E_y$ in the y direction. Public Domain, Link
**File 2.3.4 ** Hall_Effect_Measurement_Setup_for_Electrons.svg
**Result 2.3.5 ** The **classical hall field** $\vec{E}_{\text{hall}}$ for external electric field $\vec{E}_{\text{ext}}$ and magnetic field $\vec{B}$ can be written in terms of the [cyclotron frequency](https://kaedon.net/l/k3cc) $\omega_c$ and [mean scattering time](https://kaedon.net/l/73pc) $\tau$
\[\vec{E}_{\text{hall}} = \omega_c\tau(\vec{B}\times\vec{E}_{\text{ext}})\]
**Definition 2.3.6 ** The **hall coefficient** denoted $R_H$ is the measurable ratio between the hall field $E_y$ and the product of the current $J_x$ and $B_z$ applied to drive that hall field. The Drude model predicts that this quantity is related to the charge carrier density $n_e$.
\[R_H = \frac{E_y}{J_xB_z} = \frac{-\omega_c\tau E_x}{J_x B_z} = \frac{-1}{en_e}\]
### 2.4 Drude-Lorentz Gas
**Definition 2.4.1 ** The **temperature gradient** denoted $\vec{\nabla} T(\vec{r})$ is the the gradient of temperature $T(\vec{r})$ at position $\vec{r}$ in a material.
**Definition 2.4.2 ** The **heat current** denoted $\vec{j}_q$ is the rate of energy transfer through a material due to temperature gradient.
**Definition 2.4.3 ** The **thermal conductivity** denoted $k$ of a material is the coefficient that relates the temperature gradient $\nabla T$ to the heat current $\vec{j}_q$.
\[\vec{j}_q = -k\sigma \vec{E}\]
**Definition 2.4.4 **
**Definition 2.4.5 **
**Result 2.4.6 **
**Result 2.4.7 **
**Result 2.4.8 **
**Result 2.4.9 **
**Result 2.4.10 **
**Definition 2.4.11 ** \[\text{DYNAMIC EQUATION}\]
\[\text{Equilibrium Condition}\]
**Definition 2.4.12 ** linear response coefficients
**Result 2.4.13 ** electric conductivity, heat conductivity, seabeck
**Result 2.4.14 ** Drude-Lorentz Heat capacity
**Definition 2.4.15 ** The **Lorentz number** denoted $L$ is the proportionality constant that relates the thermal conductivity $\kappa$ to the electric conductivity $\sigma$ at temperature $T$.
\[L = \frac{\kappa}{\sigma T}\]
**Law 2.4.16 ** The **Wiedemann–Franz law** states that the [Lorentz number](https://kaedon.net/l/217r) $L$ is a constant that can be written in terms of the Boltzmann constant $k_B$ and the elementary charge $e$.
\[L = \frac{\kappa}{\sigma L} = \frac{\pi^2}{3}\left( \frac{k_B}{e} \right)^2\]
### 2.5 Transparency
**Definition 2.5.1 **
### 2.6 Sommerfeld Model
**Definition 2.6.1 **
**Definition 2.6.2 **
## 3 Geometry and Constitution of Solids
**Section 3.1 **
**Section 3.2 **
**Section 3.3 **
**Section 3.4 **
## 4 Electrons in Solids
**Section 4.1 **
**Section 4.2 **
**Section 4.3 **
**Section 4.4 **
## 5 Disorder and Defects
**Section 5.1 **
**Section 5.2 **
**Section 5.3 **
## 6 Topology
**Section 6.1 **
**Section 6.2 **
**Section 6.3 **